Physical Computing @ROSiE LAbs

2017, Sep 11    

La costante di Planck rilevata sperimentalmente

Il lettore potrà apprezzare quanto sia fondamentale la formula di Einstein scoperta nel 1905, che gli valse il premio Nobel nel 1921.

La costante \(h\), fondamentale per la teoria quantistica (a livello atomico), è la costante di Planck, che la propose nel 1900.

Le sue dimensioni sono Joule * secondi, se l’energia viene misurata in Joule e la frequ4nza in oscillazioni al secondo.

Il suo valore è \(h = 6,626068 10^{–34} J\cdot s\).

Il lettore noti che la “fisica classica”, quella delle leggi di Newton e di Maxwell, vale piuttosto bene fintanto che il prodotto dell’energia per il tempo dà un risultato sensibilmente maggiore di h.

Rare Book, Physical Review, vol. 7, Issue 3, pp. 355-388 - Millikan R.A. - 1916

Motivazioni.

Planck era interessato a spiegare lo spettro continuo emesso dai corpi solidi caldi, ovvero lo “spettro di corpo nero”, chiamato così poiché si considera emesso da un oggetto caldo ideale (appunto, il “corpo nero”).
L’esperienza quotidiana (un prato è verde, i mattoni sono rossi) insegna che un oggetto solido riscaldato emette luce avente una frequenza dominante, che si sposta gradualmente verso la zona blu dello spettro al crescere della temperatura; esempi come un ferro rovente lavorato da un fabbro, il colore del quale ferro ulteriormente riscaldato sposta la luce emessa dal rosso cupo all’arancione, oppure la luce infrarossa emessa da una mano umana calda, o ancora una lampadina che normalmente brilla di luce bianco-gialla, spostandosi verso l’arancione se la batteria che la alimenta si sta scaricando, e, infine, l’arco voltaico che si produce tra du elettrodi di carbone attraversati da una forte corrente, si colora di luce blu-ultravioletta, la cui frequenza è nociva per l’occhio umano.

Il metodo di misura

Si sfrutta l’emissione luminosa da parte dei dispositivi a semiconduttore noti come LED.

Attraverso la giunzione p-n del diodo LED verrà fatta scorrere una corrente diretta; gli elettroni, ricombinandosi con le lacune in prossimità della giunzione, produrranno fotoni di energia \(E\cdot \nu\) prossima al valore dell’energy gap (l’intervallo dellle energie proibite situate tra la banda di valenza e quella di conduzione). L’energia di questi fotoni emessi è data dal dal lavoro fatto dal campo elettrico \(V_{LED}\cdot e\) applicato alla giunzione polarizzata direttamente (quadrante I).

1.1

Fig.1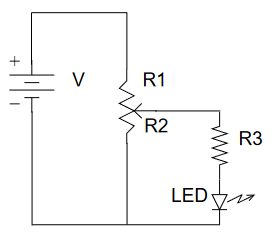

Scopo dell’esperimento

Calcolare la tensione di innesco del led, ovvero la differenza di potenziale che causa l’accensione del diodo LED, necessaria, quindi, a calcolare e a verificare la costante di Planck.

Materiale utilizzato

• Geogebra, per elaborare i grafici
• Arduino
• Basetta sperimentale
• Voltmetro
• Amperometro
• Potenziometro
• Cavi e resistore
• 3 led (verde, giallo, rosso)

Descrizione delle varie fasi dell’esperimento:

• Fase 1: Preparazione dell’H/w (inserire anche una foto del progetto reale) Si utilizzao 3 led (verde, giallo, rosso), una breadboard, una resistore, vari cavi e un potenziometro e Arduino.
• La tensione di attivazione del diodo LED:
  • Metodo 1. All’interno di una camera oscurata si misura la tensione ai capi dei terminali anodo e catodo con un voltmetro, rilevando questa tensione elettrica di attivazione nel momento in cui il diodo LED emette luce.
  • Metodo 2. Determinazione della caratteristica I-V del diodo LED, estrapolando la tensione al ginocchio di detta curva:
    • Metodo 2a. Manualmente, individuando due punti corrente-tensione, tracciando i punto di attivazione del diodo LED.
    • Metodo 2b. Automatizzando il tracciamento della curva caratteristica V-I del diodo LED con l’uso di un \(\mu C\) ed estrapolando la tensione di attivazione.

Dalla formula 1.1 si ricava:

Dal grafico ottenuto riportando i dati dalla tabella, si ricava \(\frac{V_{LED}}{\nu}\) come il reciproco della pendenza della retta \(y = m \cdot x + n\).

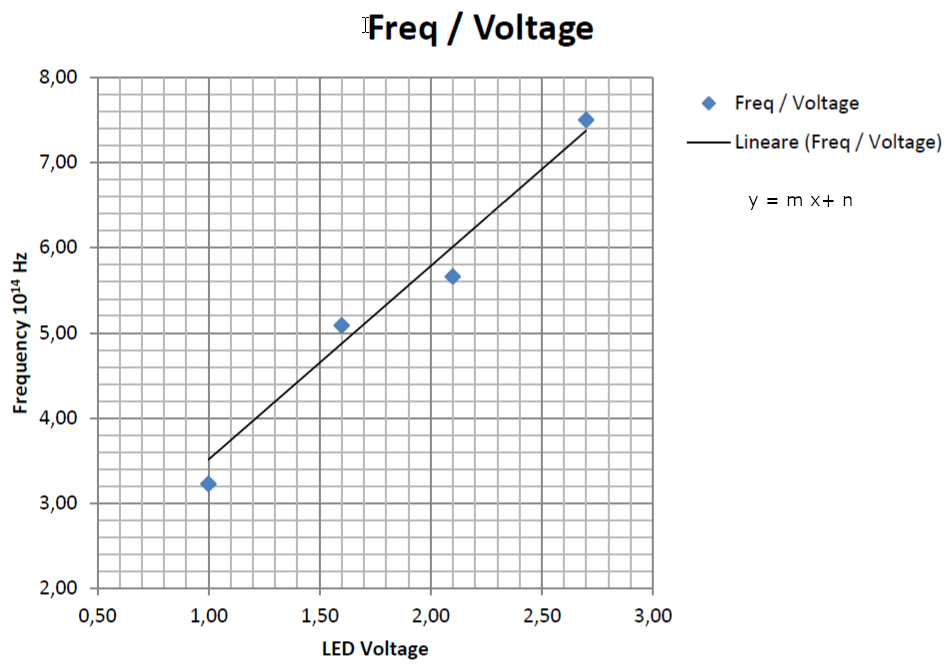
Metodo 2b.

Sono noti i seguenti dati: \(q= 1,602 \cdot 10^{-19} C\) (valore elementare della carica elettrica), \(\lambda\) (lunghezza d’onda della luce emessa dal diodo LED) e \(c\) (velocità della luce), \(k = 1,3806488 \cdot 10^{-23} J/K\) (la costante di Boltzmann).

L’esperimento si svolgerà in modo tale da trovare il valore \(V_{LED}\) che rappresenta la tensione di attivazione del diodo LED.

Fig.2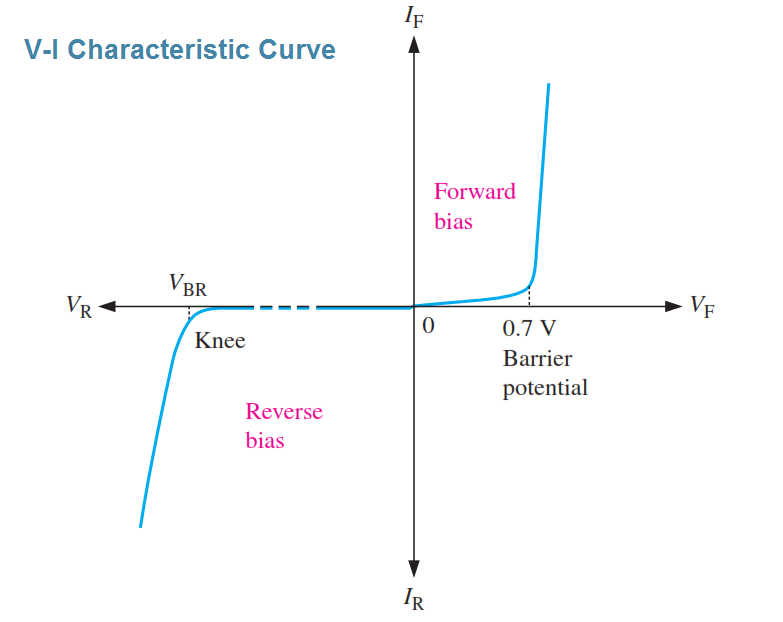

Il grafico è rappresentato dalla seguente espressione matematica, ove l’incognita è \(V\):

Ricavare le coppie (V,I) ottenuto variando il valore R del circuito rappresentato nella figura Fig.1.

Fig.3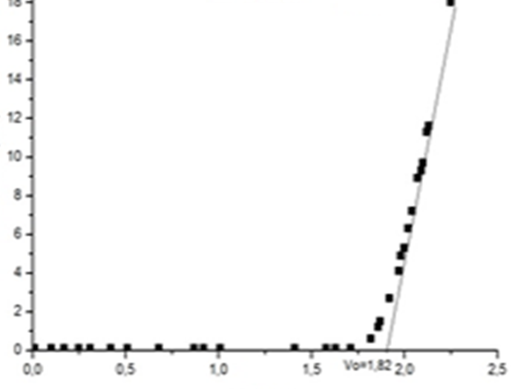

i) Effettuare una regressione lineare sui punti ricavati nella Fig.3, per trovare il valore \(V_{LED}\) di attivazione.

Utilizzando un sistema di acquisizione automatica di dati tramite l’utilizzo di un micro-controllore è possibile ottenere la caratteristica V-I di un diodo LED molto densa di coppie (I, V): la seguente figura mostra tre diverse caratteristiche V-I di tre diodi LED, di colore rosso, verde e blu.

Fig.4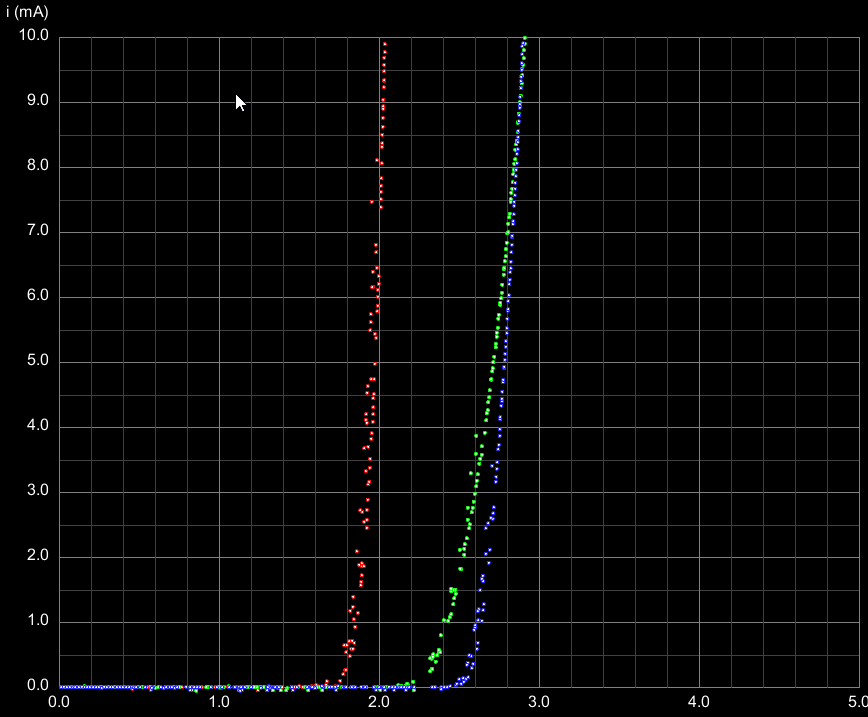

La regressione lineare \(y = m\cdot x + n\) comporta per i tre diodi LED:

diodo LED	m	m_error	n	error_n	\(V_{LED}\)	\(\lambda\) (nm)
Rosso	3.38014	+/- 0.2823 (8.352%)	-2.31808	+/- 0.4436 (19.14%)	1.678	685
Verde	2.55754	+/- 0.1625 (6.356%)	-2.49641	+/- 0.3437 (13.77%)	2.285	575
Blu	2.21159	+/- 0.1685 (7.621%)	-2.15497	+/- 0.3618 (16.79%)	2.473	490

Segue una brevissima video clip che riprende l’acquisizione a \(\mu C\) della caratteristica V-I di un diodo LED.

che comporta per i tre diodi LED

diodo LED	h	h_error
Rosso	\(6.23\cdot10^{-34}\)	+/- … (…%)
Verde	\(6.86\cdot10^{-34}\)	+/- … (…%)
Blu	\(6.44\cdot10^{-34}\)	+/- … (…%)

Se ne deduce, allora, il valore misurato attendibile per \(h\):

Si lascia al lettore il calcolo dell’incertezza delle misure.

oppure

ii) Presi due punti sul grafico, si sostituiscono le loro coordinate (y, x) nell’equazione del diodo LED, risolvendo per la quantità \(\frac{q}{\eta kT}\) e per \(I_S\)….in progress.